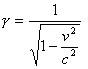Jellal schreef:
(...)
de lorenzfactor is erg onduidelijk wat ze nou precies willen dus het zal allemaal wel, het driehoeksmeting zou wel nice zijn als het je niet te veel tijd kost
Oké, de driehoeksmeting maakt gebruik van het feit dat de vorm van een driehoek vastligt wanneer de basiszijde en de hoeken van de twee punten bekend zijn (HZH) -om dit te checken of te begrijpen kan je altijd even proberen om verschillende driehoeken te tekenen met één zijde van 4 cm en aanliggende hoeken waarvan de linker hoek 40 graden en de rechter 70 graden is. Dat gaat je niet lukken.
De driehoeksmeting heeft twee vormen: voorwaartse insnijding en achterwaartse insnijding.
Voorwaartse insnijding hoe ik het heb geleerd:
(Ik heb het alleen geleerd met een horizontale bekende zijde helaas, anders moet je met het argument werken, maar dat heb ik nooit hoeven doen. Hij is horizontaal als de Y waarden van de twee bekende coördinaten gelijk zijn)
Je kan de plaats van het derde punt bepalen wanneer je de coördinaten en hoeken van de twee andere punten weet. Stel je hebt een driehoek met de punten A, B, en C. Van A en B weet je de coördinaten en van de bijbehorende hoeken a en b weet je de graden.
Stap 1: Zijde AB kan je dan ook bepalen door middel van de stelling van pythagoras (wortel van (XB-XA)^2+(YB-YA)^2).
Deze stap moet sws zo, ook als je met het argument werkt!
Stap 2: Daarna gebruik je de sinusregel om of zijde AC of zijde BC uit te rekenen. De sinusregel:
AB/sin c = AC/ sin b = BC/ sin a
AC=(ABxsin b)/sin c
BC=(ABxsin a)/sin c
(De hoeken a en b zijn bekend en de hoek c kan je uitrekenen door 180-a-b te doen)
Stap 3: De coördinaten berekenen
XC=XA+(ACxcos a)
YC=YA+(ACxsin a)
of
XC=YB+(BCxcos b)
YC=YB+(BCxcos b)
Dus de coördinaten van punt C zijn (XC,YC).
Ik probeer nog uit te vinden hoe het met het argument moet, maar snap je dit iig? Achterwaartse insnijding heb ik volgens mij ook niet gehad, dus ook dat ben ik nog even aan het uitvogelen c;
[ bericht aangepast op 20 jan 2015 - 20:39 ]
Happy Birthday my Potter!